Factorización II Ejercicios Resueltos
ASPA DOBLE
Forma genera:
Si le faltase un término, completar con el cero
Procedimiento:
Paso 1: Aspa simple a los términos: t1; t2 y t3 .
Paso 2: Aspa simple a los términos : t3; t5 y t6 .
Paso 3: Aspa simple de comprobación: t1; t4 y t6.
Paso 4: Los factores se adoptan horizontalmente.
ASPA DOBLE ESPECIAL
Forma general:
Si le faltase un término, completar con el cero.
Procedimiento
Paso 1: Descomponer los términos “t1” y “t5” de modo que el producto en aspa determine un término cuadrático.
Paso 2: Descomponer el término que resulta de hacer la diferencia del término central y el término cuadrático obtenido en el paso 1.
Paso 3: Si esta expresión fuese correcta, al multiplicar en aspa debe verificar los términos segundo (t2) y cuarto (t4).
Paso 4: Los factores se adoptan horizontalmente.
DIVISORES BINÓMICOS
Se utiliza para factorizar polinomios de grado mayor o igual a tres.
Procedimiento:
Paso 1: Determinar el rango de aquellos posibles valores que anulan al polinomio. Si el coeficiente principal del polinomio es uno (polinomio mónico), se trabaja con:
Si no es mónico el polinomio, usaremos.
Paso 2 : En base a estos valores realice evaluaciones hasta conseguir algún valor que logre anularlo.
NOTA: Todo valor que anula al polinomio genera un factor de 1er grado.
Paso 3: Para conseguir el otro factor o factores. aplicaremos Ruffini cuántas veces sea necesario.
PROBLEMAS RESUELTOS
01. Factorizar
02. Indicar un factor de:
03. Factorizar:
04. Factorizar:
ASPA DOBLE ESPECIAL:
05. Factorizar:
06. Factorizar:
07. Indicar un factor de:
08. Indicar un factor de:
09. Indicar un factor de:
10. Factorizar:
11. Indicar un factor de:
12. Indicar un factor de:














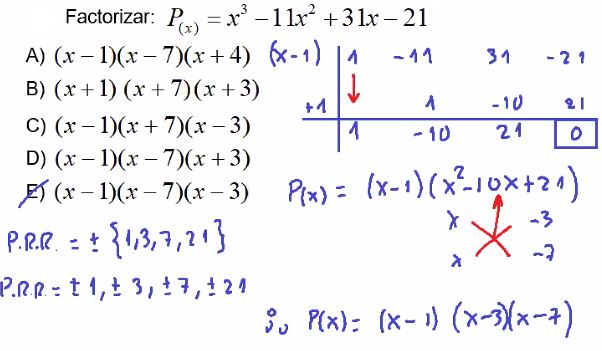



.png)



