R.T. de Ángulo en posición normal.
CONOCIMIENTOS PRINCIPALES
1. ÁNGULO EN POSICIÓN NORMAL
Es un ángulo trigonométrico cuyo vértice es el origen de
coordenadas, cuyo lado inicial (L.I.) coincide con el semieje
de las abscisas y cuyo lado final (L.F.) nos indica el
cuadrante al cual pertenece. También se le denomina
ángulo en posición estándar o en posición canónica.
Ejemplos:
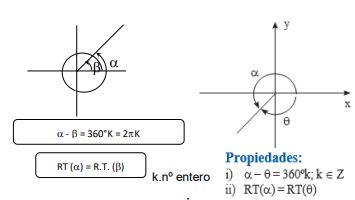
2. ÁNGULOS COTERMINALES
Son ángulos en posición normal que tienen el mismo lado
final.
3. RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO ESTÁNDAR CUALQUIERA
Se define razón trigonométrica de un ángulo estándar a la
relación o cociente que se establece entre la abscisa (x),
ordenada (y) y radio vector (r) de un punto que pertenece al
lado final del ángulo.
4. ÁNGULO CUADRANTALES
Son aquellos ángulos en posición normal, cuyo lado final
coincide con cualquier de los 4 semiejes coordenados. Los
ángulos cuadrantales no pertenecen a ningún cuadrante.
5. RAZONES TRIGONOMÉTRICAS DE LOS ÁNGULOS CUDRANTALES
6. SIGNOS DE LAS RAZONES TRIGONOMÉTRICAS
Ejercicios Resueltos
1.- Calcula el cosθ en la figura:
Desarrollo:
2.- Calcula: secθ - tanθ
Desarrollo:
3.- Calcula: “cotθ” ; si senθ = 1/3 y θ II ∈ C
4.- Si: senα= -2/3 ∧ α ∈ IIIC.
5.- Calcula el valor de: E = 3sen90° + 5cosπ + 2tan2π
6.- Calcula el valor de: E = cos(senπ) + sec(tan0°)
7.- Si : tanθ = 2,4. Halla : “senθ” además cosθ < 0
8.- Si: cosα = 40/41 y α ∈ IV C, Halla : E = cscα + cotα
9.- Del gráfico calcule: E = 25senα + tgθ
Desarrollo:
.png)



















.png)



