Circunferencia II Ejercicios Resueltos
ÁNGULOS EN LA CIRCUNFERENCIA
Ángulo Central
Ángulo Inscrito
Ángulo Ex – inscrito
Ángulo Semi – Inscrito
Ángulo Interior
Ángulo Exterior
EJERCICIOS RESUELTOS
1. Calcular x, si mAPB = 300º
2. Calcular “x”, si “O” es centro
3. Calcular “θ” siendo A y B puntos de tangencia.
4. Calcular “α”
5. Calcular “x”. Si mBC = 100º y A es punto de tangencia.
6. Hallar la mAC = si mBD = 150º
7. Calcular “x”, si “O” es el centro.
8. En el gráfico. Calcular “x”.
9. Calcular “x”
10. En la figura mostrada, hallar los valores de los arcos AF y PQ.
11. Calcular “x”, si “O” es centro (A y B son puntos de tangencia)
12. La circunferencia está inscrita en el ∆PBC. Calcular “θ”.
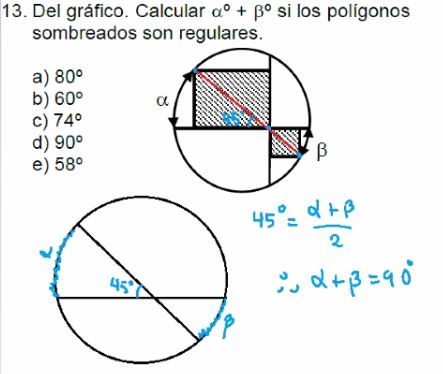
13. Del gráfico. Calcular αº + βº si los polígonos sombreados son regulares.
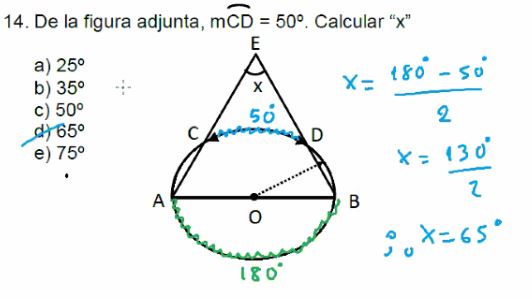
14. De la figura adjunta, mCD = 50º. Calcular “x”
15. Se tiene un triángulo ABC, en el cual la circunferencia que pasa por los puntos medios de sus tres lados pasa también por el vértice B. Calcular la m B .
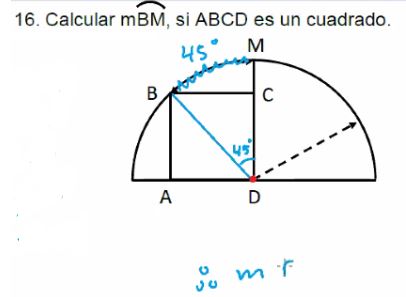
16. Calcular mBM, si ABCD es un cuadrado.
17. En la figura el triángulo ABC es isósceles (AB = BC) y m<BCD = 20°, calcular:
18. Hallar “x” si α + β = 133°. “O”: centro.
19. Si: TP = 4 y AB = 6, calcular mTL.
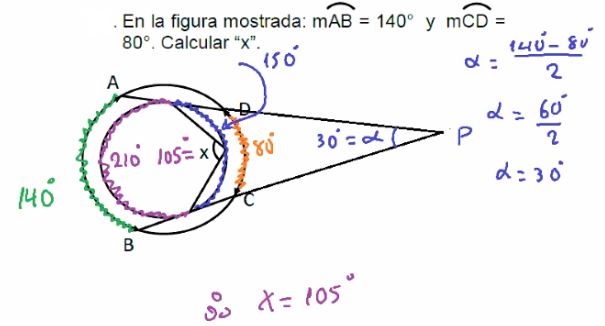
20. En la figura mostrada: mAB = 140° y mCD = 80°. Calcular “x”.
21. Hallar “x”, si P = 50°.
22. En la figura AMNC es un trapecio isósceles (AM = NC) y m<BQA = 110°, calcular m<BAQ. (A es punto de tangencia).
23. Calcular “x”, sabiendo que: m<BAC = 40°.
24. En la figura: AD = DE y m<ABR = 25°. Calcular la m<DCE (A y C: puntos de tangencia).




























.png)



