Ángulos entre paralelas Ejercicios resueltos
RECTAS PERPENDICULARES
1.1. DEFINICIÓN.
Se dice que dos rectas son perpendiculares cuando al cortarse forman cuatro ángulos iguales. Cada uno es un ángulo recto. El símbolo de perpendicular es: ⊥ Si dos rectas se cortan y no son perpendiculares se dice que son oblicuas.
2. RECTAS PARALELAS
2.1. DEFINICIÓN
Se dice que dos rectas de un plano son paralelas cuando al prolongarse no tienen ningún punto común. El paralelismo tiene la Propiedad Recíproca, es decir: si una recta es paralela a otra, esta otra es paralela a la primera. El símbolo de rectas paralelas es //.
O también las rectas paralelas se pueden expresar de la siguiente manera:
3. RECTAS SECANTES
3.1. DEFINICIÓN
Dos rectas en un plano son secantes cuando tienen un punto en común.
4. ÁNGULOS FORMADOS POR DOS PARALELAS Y UNA SECANTE
Dos rectas paralelas al ser cortadas por una tercera recta (llamada recta secante) determinan ángulos especiales por la posición de uno respecto al otro.
Los cuatro ángulos determinados en la recta L1 se relacionan con los cuatro ángulos determinados en la recta L2 formando parejas que reciben nombres específicos. Es importante identificar tales parejas y conocer sus propiedades. Los ángulos formados son:
5. PROPIEDADES
PROBLEMAS RESUELTOS
1. En la figura calcula “x”, sí L1 // L2.






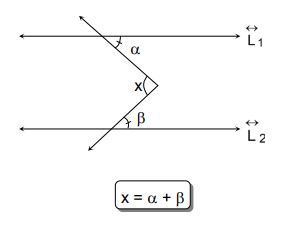















.png)



