Proporcionalidad de segmentos Ejercicios Resueltos
RAZÓN DE SEGMENTOS
SEGMENTOS PROPORCIONALES
TEOREMA DE THALES
Tres o más rectas paralelas, determinan en una recta secante a ellas, segmentos que son proporcionales, a los segmentos determinados por las mismas rectas paralelas en cualquier otra secante a ellas.
COROLARIO
TEOREMA DE LA BISECTRIZ INTERIOR
En todo triángulo, los lados concurrentes con una bisectriz interior son proporcionales a los segmentos determinados por dicha bisectriz en el lado al cual es relativa.
TEOREMA DE LA BISECTRIZ EXTERIOR
En todo triángulo, los lados concurrentes con una bisectriz exterior son proporcionales a los segmentos determinados por dicha bisectriz en el lado al cual es relativa.
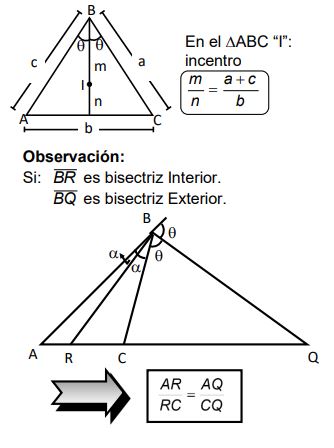
TEOREMA DEL INCENTRO
En todo triángulo el incentro determina en la bisectriz segmentos proporcionales a la suma de los lados adyacentes al ángulo bisecado y el tercer lado.
Ejercicios Resueltos
1. Si: L1 // L2 // L3. Calcular: “x”
2. L1 // L2 // L3. Calcular EF, Si: AC = 12, AB = 3 y DF = 48.
3. Calcular: MA, MN // AC . Si: AB = 12, BC = 16, BN = 7.
4. Hallar: “ω”, MN // AC
5. En la figura: AB = 8, BC = 6 y AC = 7. Calcular: AM
6. Calcular: BR. Si: BC = 12.
7. En la figura. Calcular: CE. Si: AB = 8, BC = 6, AC = 7.
8. En la figura, Hallar AB. Si: BC = 2, AD = 9 y CD = 6.
9. Calcular: QR. Si: AB = 8, BC = 6 y AC = 7.
10. Calcular: CF. Si: AE = 5, EC = 3 y m ^ EBF = 90º.
11.En un trapezoide ABCD las bisectrices de los ángulos B y D se cortan en un punto E de la diagonal AC . Si: AB = 15, BC = 10 y CD = 12. Calcular: AD.
12. En un triángulo ABC, BD y BE son bisectrices, interior y exterior respectivamente. Calcular CE. Si AD = 5 y DC = 3.
13.En un triángulo ABC, AB = 18, se traza la mediana BM. Calcular: BM. Si: m M B ˆ C = m A ˆ + m C.
14. En un triángulo ABC de lados AB = 2, BC = 5 y AC = 3,5, se traza la bisectriz BS. Calcular: (SC - AS).
15. Hallar “BC”, MB = 2, AM = 6
16. En el gráfico, AB = 6u, BC = 9u, CD = 7u. GH – EF = 2u. L1 // L2 // L3. Hallar FG.
17. En un triángulo ABC, se traza la paralela EF a AC (E e AB y F e BC ), si : BF = 4 , FC = 3 y AE = 15/4. Hallar EB.
18. En la figura se cumple que:
19. Del gráfico, calcular x si L1 // L2 // L3 y AE // BD.


























.png)



