Productos notables Ejercicios Resueltos
PRODUCTOS NOTABLES
Los productos notables son fórmulas que permiten efectuar multiplicaciones indicadas, sin aplicar los criterios generales de la multiplicación algebraica, y deben satisfacer las siguientes propiedades:
PROPIEDAD 1
El grado del producto es igual a la suma de los grados de los factores, en efecto:
Ejemplo. 1: Hallar el grado de P(x)
Solución:
Observemos que el grado en cada paréntesis es:
Ejemplo 2: Hallar el grado de R(x)
Solución:
Para este caso, el grado correspondiente en cada paréntesis es:
PROPIEDAD 2
El término independiente del producto es igual al producto de los términos independientesde los factores, es decir:
Ejemplo 1: Hallar el término independiente de P(x) en:
Solución:
El término independiente en cada paréntesis es:
Ejemplo 2: Hallar el término independiente de P(x) en:
Solución:
En este caso, el término independiente en cada paréntesis es:
Para un entendimiento coherente respecto a los productos notables y las identidades, los observaremos por grupos:
GRUPO: I
I. Cuadrado del Binomio
II. Cubo del Binomio
Estas mismas fórmulas se pueden expresar bajo las formas:
III. Diferencia de cuadrados (suma por diferencia)
IV. Suma y Diferencia de cubos
Ejemplos:
01. Efectuar
Solución:
Teniendo en cuenta que:
Entonces:
02. Simplificar:
Solución
Dado que:
03. Calcular:
Expresando convenientemente, se tendría:
Operando por partes:
Con lo cual, se tendría:
4. Si:
Solución
Elevando la condición al cubo, se obtiene:
EJERCICIOS RESUELTOS
1. Si:
2. Si:
3. Si:
4. Si:
5. Si:
6. Si:
7. Simplifique:
8. Simplifique:
9. Halle el valor numérico de:
Parte 2: https://pit4goras.blogspot.com/2022/01/productos-notables-ii-ejercicios.html














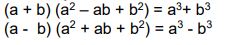


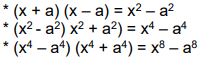


















.png)



