Triángulos II Ejercicios Resueltos
1. CEVIANA
Es el segmento que une un vértice de un triángulo con un punto cualquiera del lado opuesto o de su prolongación. Desde un vértice se puede trazar infinitas cevianas. Por lo tanto, las ceviana no es línea notable. El nombre de ceviana se debe en honor al matemático italiano CEVA en 1678.
2. MEDIANA
Es una ceviana interior que divide al lado opuesto en partes iguales.
BARICENTRO(G):
Llamado también centro de gravedad o gravicentro o centroide, es el punto de concurrencia de las tres medianas de un triángulo. El Baricentro, siempre es un punto interior al triángulo, divide a cada mediana en dos segmentos que están en la relación de 1/3 y 2/3 de la mediana.
3. BISECTRIZ INTERIOR
Es el rayo que, partiendo del vértice de un triángulo, divide al ángulo interior en 2 ángulos de igual medida.
Bisectriz Exterior:
Es el rayo que, partiendo del vértice de un triángulo, divide al ángulo exterior en 2 ángulos de igual medida.
4. ALTURA
Es el segmento perpendicular trazado desde un vértice del triángulo a la recta que contiene al lado opuesto. En cada una de las siguientes figuras, el segmento BH es una altura del triángulo ABC.
Triángulo Acutángulo
Triángulo Obtusángulo
Triángulo Rectángulo
5. MEDIATRIZ
Es una recta perpendicular a un lado del triángulo en su punto medio, dicha recta se encuentra en el mismo plano que contiene al triángulo
PROPIEDADES CON LÍNEAS NOTABLES
PROPIEDADES PARTICULARES
EJERCICIOS RESUELTOS
01. Si BH es altura del triángulo ABC, calcular “x”
02. Si AB = BC, calcular “x”
03. Si BD es bisectriz del ángulo ABC, calcular “x”
04. En el triángulo ABC: m<B=80, calcular la medida del ángulo que forman las mediatrices de AB y BC.
5.
06. Del gráfico calcular “x”.
07. Si BM es mediana del triángulo ABC, calcular “x”
08. En un triángulo ABC: m<A=80 y m<C=30; la mediatriz de AC y bisectriz exterior del ángulo B se intersecan en “P”. Calcular la m<BPM, si “M” es el punto medio de AC
09. Si m<A – m<C=50, calcular “x”
10. En un triángulo las medidas de dos de sus lados suman 28. Calcular el mayor valor entero que puede tomar la medida de la altura relativa al tercer lado.
11. Si BQ=5, calcular “BP”
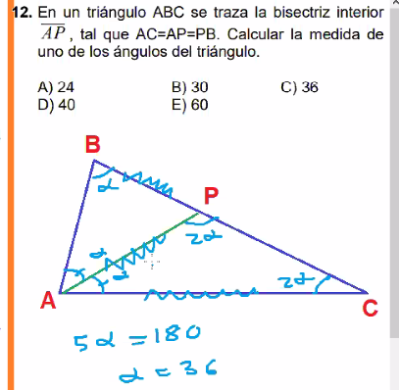
12. En un triángulo ABC se traza la bisectriz interior AP , tal que AC=AP=PB. Calcular la medida de uno de los ángulos del triángulo.























.png)



