Congruencia de triángulos Ejercicios Resueltos

Un triángulo es congruente con otro, sí y sólo sí, existe una correspondencia entre sus vértices de modo que sus lados y ángulos sean respectivamente congruentes con los lados y ángulos del otro. Según esto se tiene:

CASOS O CRITERIOS DE CONGRUENCIA

Son las condiciones mínimas para que dos triángulos sean congruentes.

Primer Caso – LAL (lado – ángulo – lado)

Si dos triángulos tienen respectivamente congruentes dos lados y el ángulo comprendido, entonces dichos triángulos son congruentes.

Segundo Caso – ALA (ángulo – lado – ángulo)

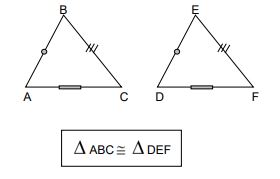
Si dos triángulos tienen respectivamente congruentes un lado y los ángulos adyacentes a este lado, entonces dichos triángulos son congruentes

Tercer caso – LLL (lado – lado – lado)

Si dos triángulos tienen respectivamente congruentes sus tres lados, entonces dichos triángulos son congruentes.

Sólo cuando se demuestre que dos triángulos son congruentes se podrá decir que a lados congruentes se oponen ángulos congruentes y recíprocamente, a ángulos congruentes se oponen lados congruentes.