Aplicaciones de la congruencia Ejercicios Resueltos
1º TEOREMA DE LA BISETRIZ DE UN ANGULO.
Todo punto que pertenece a la bisectriz de un ángulo equidista de los lados del ángulo
Demostración:
2º TEOREMA DE LA MEDIATRIZ
Todo punto que pertenece a la mediatriz de un segmento equidista de los extremos del segmento dado.
Demostración:
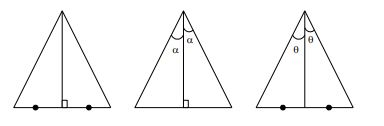
NOTA: Si dos líneas notables coinciden en un triángulo, entonces dicho triángulo es isósceles.
Ejemplo: Los siguientes triángulos son isósceles.
EJERCICIOS RESUELTOS
01. En la figura calcular “x”
02. En la figura calcular “x”
03. Calcular “x”
04. En la figura calcular “x”:
05. En la figura calcular “x”
06. En la figura: L1 // L2 calcular “x”
07. En la figura: L1: Mediatriz de AC
Si AB=MC; m<C=40; calcular m<B
8. Si α + β = 90°, calcular "x"
09. En la figura calcular “x”
10. En un triángulo ABC: Las mediatrices de AC y AB se intersectan en “O”. Si OB=4, calcular OC
11. En la figura: AJ=10 y AB=6. Calcular DH
12. En la figura:
L1: Mediatríz: de AB
L2: Mediatríz: de BC
m<ABC=100. Calcular “x”
13. En la figura calcular “x”
14. En la figura TC=2.AT. Calcular “x”
15. En la figura: L1 : Mediatriz de BD Calcular:” x”
16. En el triángulo ABC, el ángulo exterior en el vértice “B” mide 68; se trazan las mediatrices de los lados AB y BC que intersectan a AC en “R” y “S”. Calcular m<RBS
17. En la figura calcular “x”
18. En un triángulo rectángulo ABC recto en B, la mediatriz de BC intersecta a AC en “M”. Si BM=4; calcular AC.
Parte 2: https://pit4goras.blogspot.com/2022/01/aplicaciones-de-la-congruencia-ii.html























.png)



