Puntos Notables Ejercicios Resueltos
ORTOCENTRO
Es el punto de concurrencia de las alturas del triángulo, cuya ubicación depende de la naturaleza del triángulo.
En el triángulo acutángulo
En el triángulo rectángulo
En el triángulo obtusángulo
INCENTRO
Es el punto de concurrencia de las bisectrices interiores del triángulo; siempre es interior al triángulo y equidista de los lados, por lo tanto, es el centro de la circunferencia inscrita en el triángulo.
r : inradio de ABC
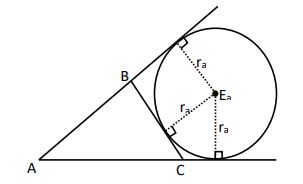
EXCENTRO
Es el punto de concurrencia de dos bisectrices exteriores y una bisectriz interior trazada del tercer vértice; se encuentra exteriormente y equidista de los lados del triángulo, por lo tanto, es el centro de la circunferencia ex – inscrita. Todo triángulo tiene tres ex – centros.
CIRCUNCENTRO
Es el punto de concurrencia de las mediatrices de los lados del triángulo, dicho punto equidista de los vértices del triángulo, por lo tanto, es el centro de la circunferencia circunscrita al triángulo. La ubicación del circuncentro depende de la naturaleza del triángulo.
En el triángulo acutángulo
En el triángulo rectángulo
En el triángulo obtusángulo
Propiedades:
Si O es el circuncentro se cumple:
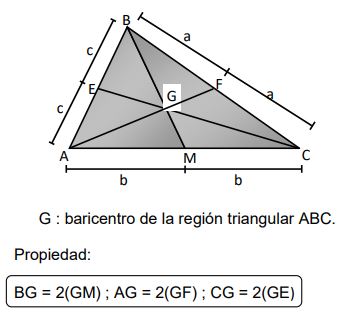
BARICENTRO
Es el punto de concurrencia de las medianas de una superficie triangular; siempre es un punto interior. El baricentro divide a cada mediana en dos segmentos, cuya razón es de dos a uno.
EJERCICIOS RESUELTOS
1. La suma de las longitudes de las medianas de un triángulo es 48 cm. Calcular la suma de las distancias del baricentro a cada uno de los vértices.
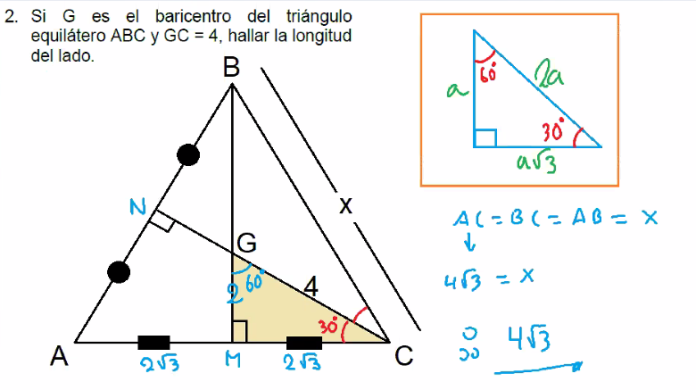
2. Si G es el baricentro del triángulo equilátero ABC y GC = 4, hallar la longitud del lado.
3. En un triángulo ABC cuyo circunradio mide 10u. Calcular AC siendo m<ABC = 37°.
4. Del gráfico, hallar x siendo K circuncentro del triángulo ABC.
5. En el triángulo acutángulo ABC se sabe que: m<A – m<C = 48°. Hallar la medida del ángulo HBO, si H es ortocentro y O es circuncentro del triángulo.
6. En un triángulo ABC, de circuncentro “K” y excentro relativo a BC “E”. Calcular m<BKC, siendo m<BEC = 50°.
7. En el gráfico mostrado, calcular x, si IM = MC. I es incentro.
8. En un triángulo ABC de incentro “I” y excentro “E” relativo a AB . Calcular la m<ABC si AE = AI.
9. En un triángulo ABC, I es el incentro y O el circuncentro. Si los ángulos AIC y AOC son suplementarios, calcular la medida del ángulo B.
10. En un triángulo ABC se ubican respectivamente su ortocentro “H”, incentro “I” y circuncentro “O” tal que 2m<AHC = 3m<AOC. Hallar m<AIC.
11. En un triángulo equilátero la distancia del baricentro al segmento que une los puntos medios de dos lados es 3 . El lado del triángulo mide:






















.png)



