Ecuaciones Cuadráticas II Ejercicios Resueltos
PROPIEDADES GENERALES
Operaciones básicas con raíces:
▪ Suma de raíces (S):
▪ Producto de raíces (P):
▪ Diferencia de raíces (D):
▪ Reconstrucción de la ecuación:
EJERCICIOS RESUELTOS
1. Hallar el valor de “P” de tal manera que la ecuación:
2. Hallar el valor de “m” en la ecuación:
3. Hallar el valor de “n” para que las raíces difieran en 1 unidad.
4. Calcular “m” en:
5. Calcular “m” en:
6. Calcule el valor de “p”, sabiendo que x1 y x2 son raíces de la ecuación:
7. Determinar los valores de “n” en la ecuación:
8. Calcule el valor de “p”:
9. Determine “m” en la ecuación:
PROPIEDADES
RAÍCES SIMÉTRICAS
Si x1 y x2 son raíces simétricas se cumplirá: x1 = A ; x2 = –A
RAÍCES RECÍPROCAS
RAÍZ NULA
ECUACIONES EQUIVALENTES
Si las ecuaciones de segundo grado tienen las mismas raíces se cumplirá:
GRÁFICA DE UNA EC. DE 2do. GRADO (PARÁBOLA)
El vértice de toda parábola tiene por coordenadas (h, k) donde:
Nota:
K = Mínimo valor del polinomio P(x) si a > 0
K = Máximo valor del polinomio P(x) si a < 0
NATURALEZA DE LAS RAÍCES
10. Si a y b son números reales de manera que las ecuaciones:
11. Determinar “m” para que la ecuación:















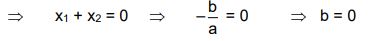









.png)



